Recientemente Wolfram Alpha ha implementado nuevas funcionalidades para mostrarnos la resolución de ejercicios paso a paso de una manera más interactiva. Veamos la solución paso a paso para una integral (una de las consultas más populares de matemáticas que se realizan). Vamos a escribir "integrate cos^2(x)" en Wolfram|Alpha y luego hacer clic en el botón de la solución paso a paso en la parte superior derecha de la página de resultados.
Para avanzar por el problema un paso a la vez, puedes hacer clic en el botón "Next step", como lo hemos hecho anteriormente. O si prefieres verlo todo de una vez, haz clic en el botón "Show all steps":
Ahora echemos un vistazo a un ejercicio elemental de matemáticas (8*11)/3 + 4, la solución paso a paso es:
Al avanzar por el problema, aparecerán sugerencias de como realizar ciertas operaciones. Si prefiere no utilizar esas sugerencias, puede hacer clic en el botón Ocultar sugerencias "hide hints" en la parte superior derecha. Y por supuesto, si quieres ver todos los pasos a la vez, puedes hacer clic en "Show all steps", como en el primer ejemplo.
La capacidad de Wolfram|Alpha para mostrar los pasos para resolver una ecuación ha crecido enormemente. Para ver esto, vamos a empezar por encontrar las raíces de un polinomio:
En la esquina superior derecha de la ventana de las soluciones "Step-bystep" hay un menú desplegable para elegir cómo vamos a resolver el problema: utilizando el método de factorización, completación de cuadrados, o utilizando la fórmula cuadrática. Vamos a probar y comparar los tres métodos:
Nuevamente, vemos que tenemos la opción de avanzar un paso a la vez (con sugerencias si quisiéramos) o mostrar todos los pasos a la vez.
Además de ofrecer sugerencias y múltiples métodos para resolver un problema, ahora podemos resolver ecuaciones sobre los números reales o sobre los números complejos! Vamos a ver esto en acción pidiendo a Wolfram|Alpha encontrar las raíces de (e^x+2)(x-1). Al resolver sobre los números reales, Wolfram|Alpha nos mostrará que (e^x+2)(x-1) tiene una sola raíz, sobre los números complejos, Wolfram|Alpha encontrará las raíces complejas de esta expresión.
Para ver aún más las nueva funcionalidades, vamos a pedir Wolfram|Alpha verificar una identidad trigonométrica. Para ello, simplemente escribes la identidad que quieres probar en Wolfram|Alpha. Por ejemplo, vamos a probar la identidad (sin (x) - tan (x)) (cos (x) - cot (x)) = (sin (x) - 1) (cos (x) - 1):
Aquí hay algunos ejemplos más para que puedas explorar el alcance de las soluciones paso a paso.
Aritmética:
Resolución de ecuaciones:
- 4x – 6 = 2x+8 solution
- solve (9^(x + 1)) – (28 (3^(x))) + 3 = 0 over the real numbers
- solve: x^4 + 2x^3 + 5x^2 + 10x + 25 = 0
Descomposición en Fracciones parciales:
- partial fraction decomposition 1/(x^2 + 4x + 3)
- 1 / (x^3 + 4x^2 + 5x + 2)
- 1 / (x^4 + 8x^3 + 22x^2 + 24x + 9) partial fraction expansion
- {{1,1,5},{1,-1,1}} row reduce
- reduced row echelon form: {{1, -3, 3, -4}, {2, 3, -1, 15}, {4, -3, -1, 19}}
- (1 + tan(x))/(1 – tan(x)) = (cos(x) + sin(x))/(cos(x) – sin(x))
- sin(x)^4 – cos(x)^4 = 1 – 2 cos(x)^2
- cot(t/2)^2 = (1 + cos(t)) / (1 – cos(t))
- limit of (x – 3) / (x^2 – 2x – 3) as x approaches 3
- (e^x – 1 – x) / x^2 as x goes to 0
- take the limit as x goes to infinity: (1 + 1/x)^x
Integrales:
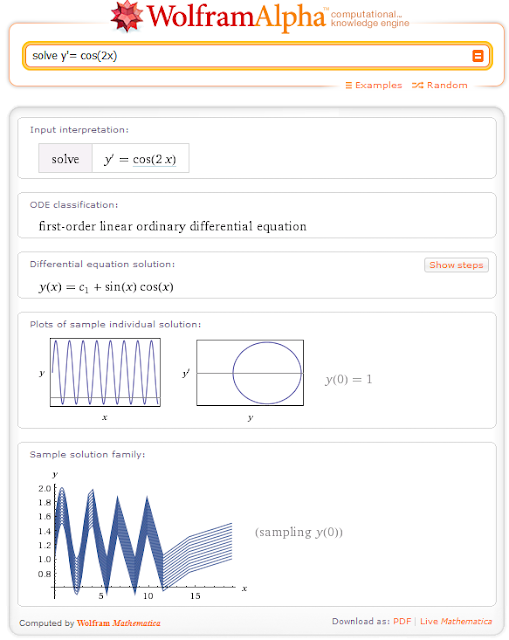
Ecuaciones diferenciales Ordinarias:
Esta es una breve descripción de lo que puedes hacer con la nueva funcionalidad "Step-by-step". Cuando te hayas registrado en Wolfram|Alpha, puedes utilizar esta nueva función gratis tres veces al día. Con Wolfram|Alpha Pro los usuarios reciben acceso ilimitado a las soluciones paso a paso.